[10000印刷√] 平行線と線分の比 平行四辺形 104282-平行線と線分の比 平行四辺形

平行四辺形の問題です 平行四辺形abcdがあります 辺abを2 3に分 数学 教えて Goo
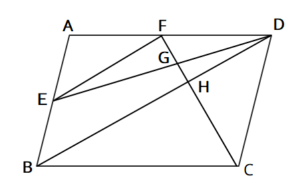
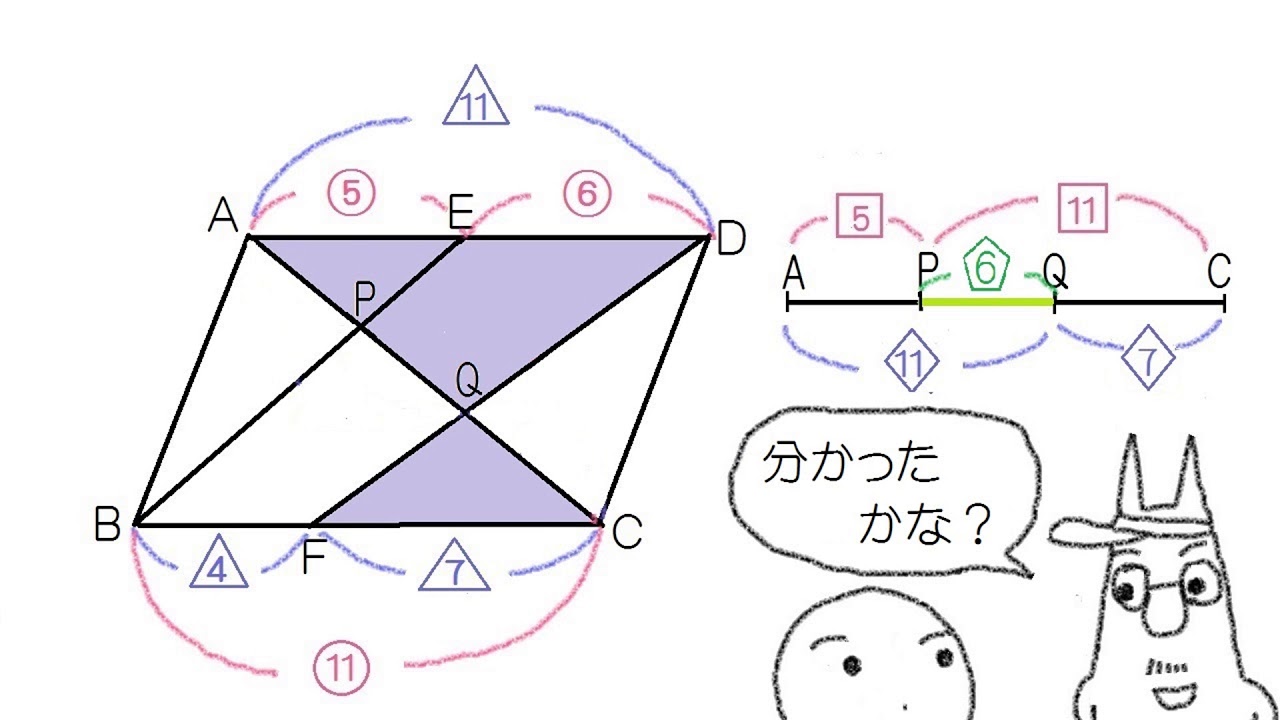
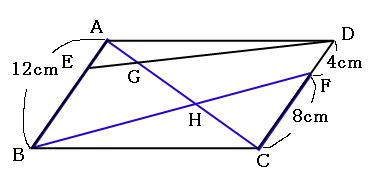
相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形abcd の辺ad 上にae:ed =1:2 となる点e をとり、e から 辺ab に平行な直線を引き、辺bc との交点をf とします。さらに、対角線ac とef動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
平行線と線分の比 平行四辺形
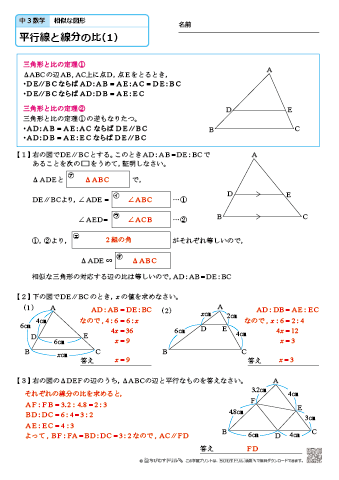
平行線と線分の比 平行四辺形-・平行線と線分の比についての性質を記号 を用いて表したり、その意味を読み取った りすることができる(技) 2 ・三角形と比の定理 の逆を証明する。 三角形と比の定理の 逆が成り立つかどう か考え、証明する ことができるように する ・平行線と線分線分 %' と線分 &( の交点を ) とする。 平行四辺形 $%&' の面積が fp のとき,四角 形 $%)( の面積を求めなさい。 33 fp fp $ ' (% ) & 右の図のような平行四辺形 $%&' があ り, %$( '$( である。 $)% の大きさを求めなさい。 ( %) の面積と平行四辺形 $&' の面積の比を最も
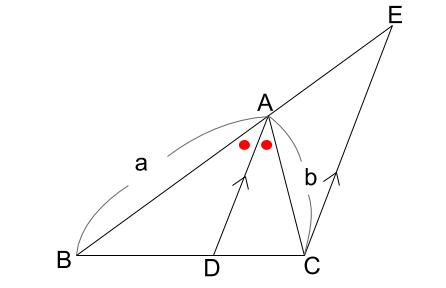
角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
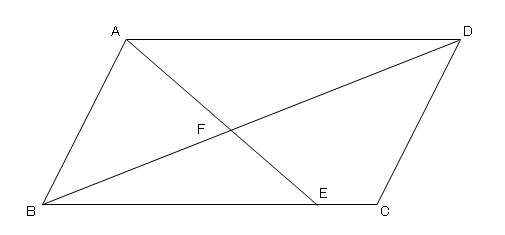
FdData 中間期末:中学数学3 年:平行線 三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内平行線と線分の比の問題の解答 以下は、ここをクリックした先の問題の解答です。 問1 上図のように、AB=10,AD=6,∠ABC<90°である平行四辺形ABCDにおいて、∠DABの二等分線と辺BCのCの方へ延長した直線との交点をEとする。 線分AEと対角線BD,辺CDと四角形decfは平行四辺形なので df=ec このことと③より addb=aeec 平行線と線分の比の証明その2 私は補助線を引いて平行四辺形を作ることが思いつかず、相似比から直接考えました。 証明 (ア)の証明より abc∽ adeであり、その相似比をabとすると
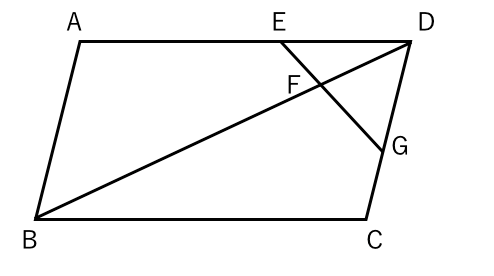
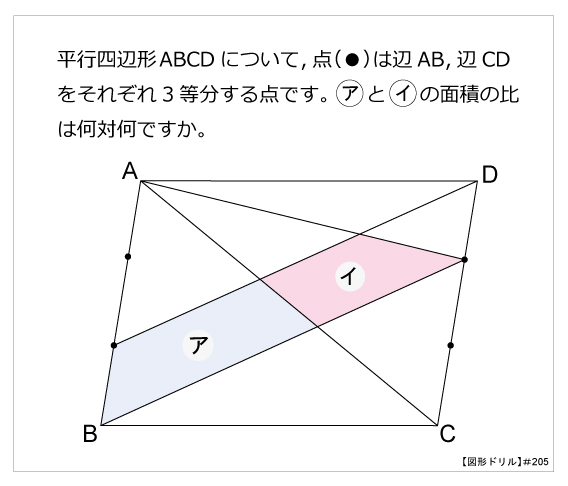
上図のように平行四辺形abcdがあります。 線分adとCBは平行四辺形の対角線です。 今、線分cd上に点Eを3:1にとり、線分beを引きました。 この時、 (三角形①の面積) : (三角形②の面積) : (三角形③の面積) の比を求めて下さい。=== 平行線と線分の比 === 三角形の相似条件 次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ. 平行線の線分比の性質を使った問題です。 図形を見てどことどこが相似になりそうかわかるようになると良いですね。 対角線が中点で交わる平行四辺形の 線分比と面積比の性質を使った問題です。 基本となるのは線分比です。 与えられた情報から
平行線と線分の比 平行四辺形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
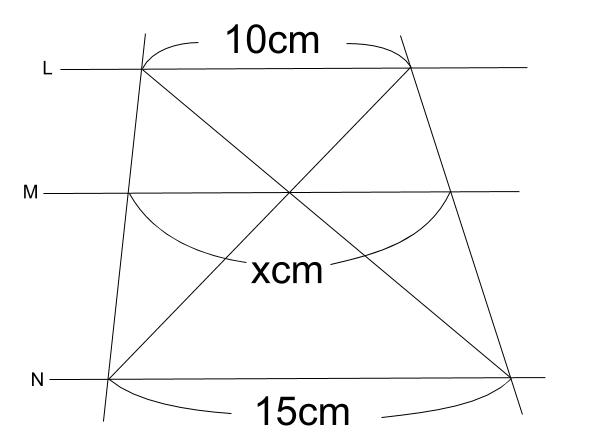 2 |  2 | 2 |
2 |  2 | 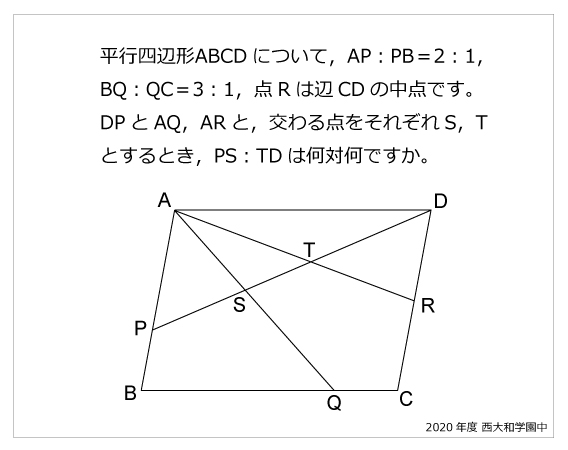 2 |
 2 | 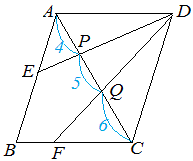 2 |  2 |
2 | 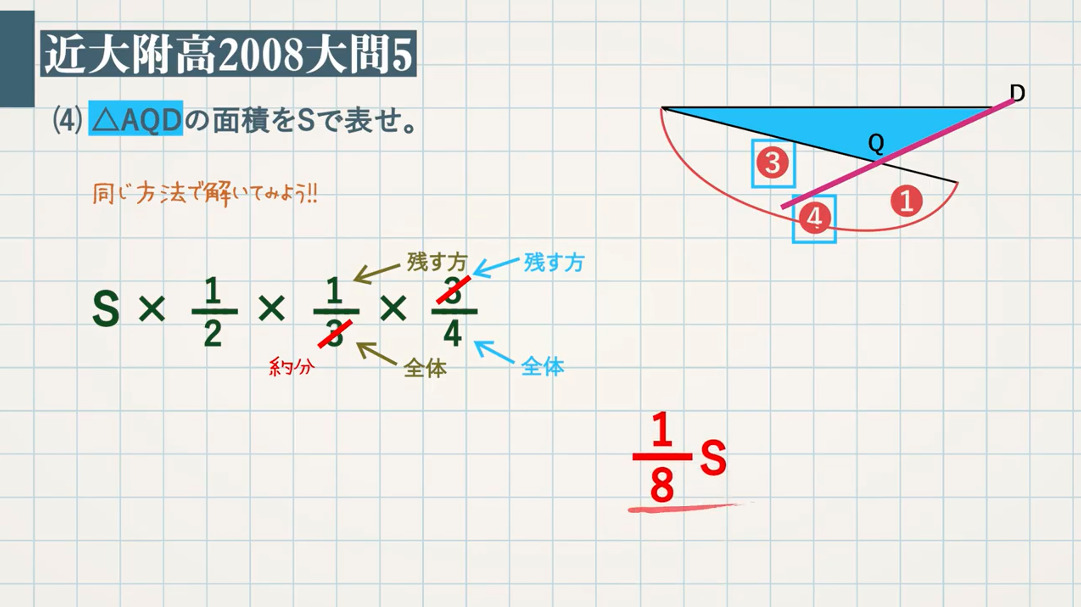 2 |  2 |
2 | 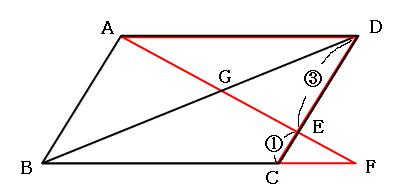 2 | 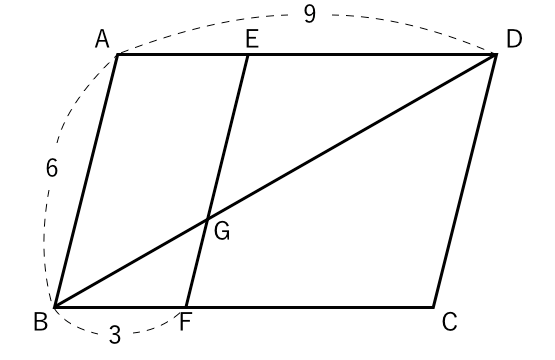 2 |
 2 |  2 |  2 |
 2 |  2 | 2 |
2 | 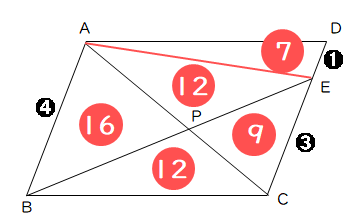 2 |  2 |
2 |  2 |  2 |
 2 |  2 |  2 |
2 |  2 | 2 |
2 | 2 | 2 |
 2 | 2 |  2 |
 2 |  2 | 2 |
 2 | 2 | 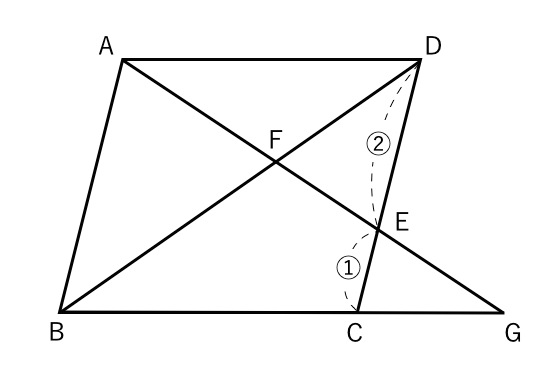 2 |
2 | 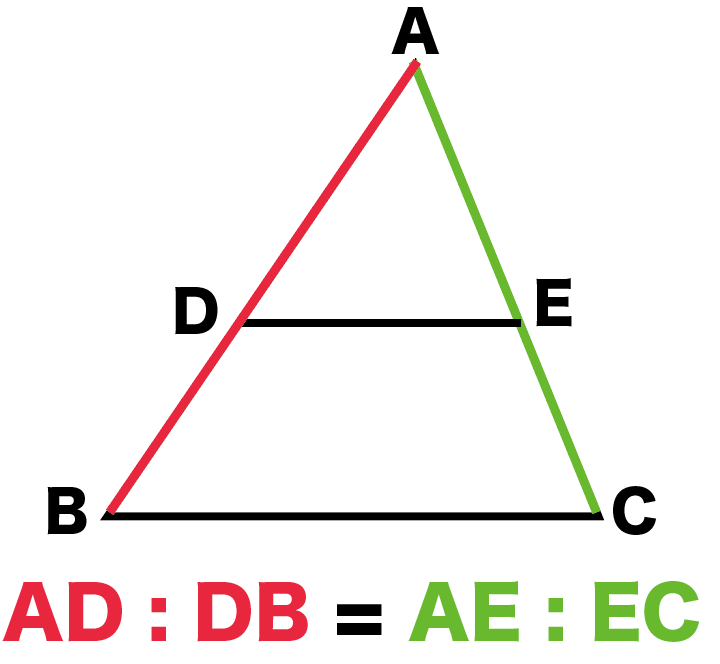 2 |  2 |
 2 |  2 | 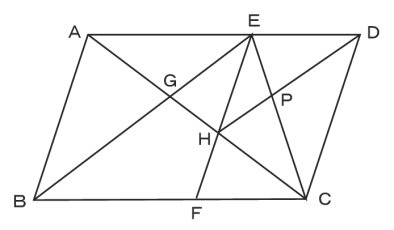 2 |
 2 | 2 |  2 |
 2 |  2 | 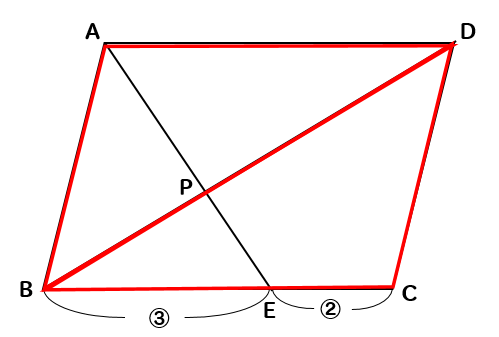 2 |
2 | 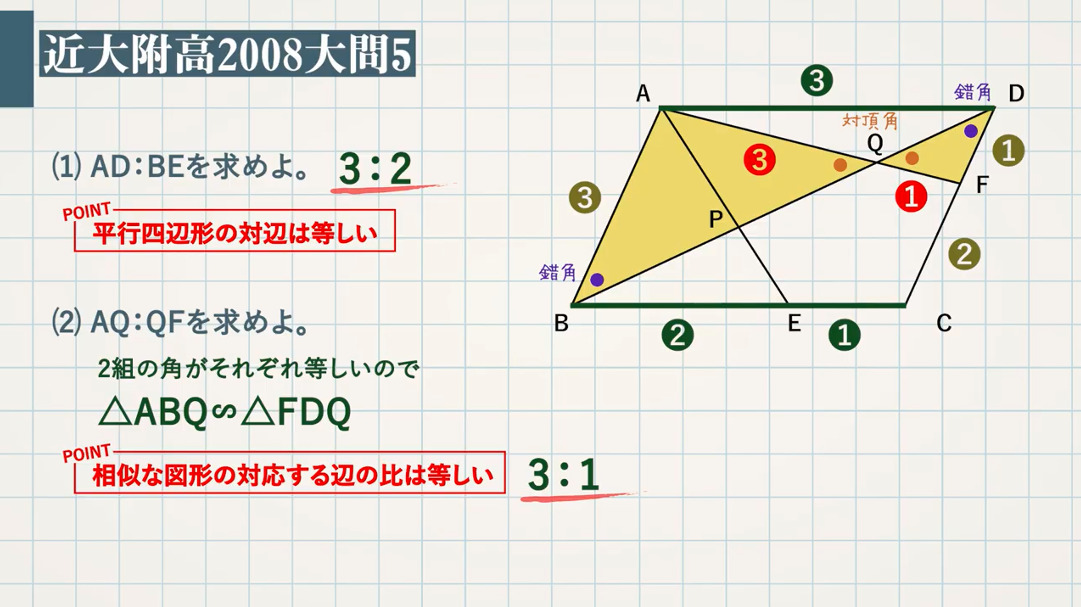 2 |  2 |
 2 | 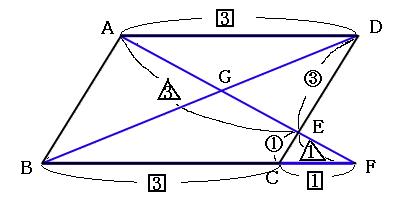 2 |  2 |
 2 |  2 | 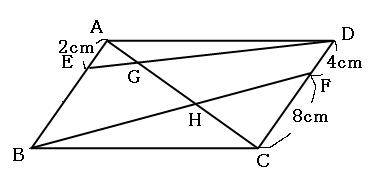 2 |
 2 |  2 |  2 |
 2 | 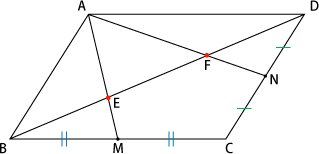 2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 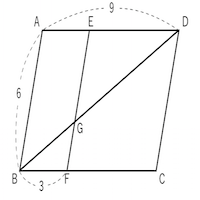 2 |
2 | 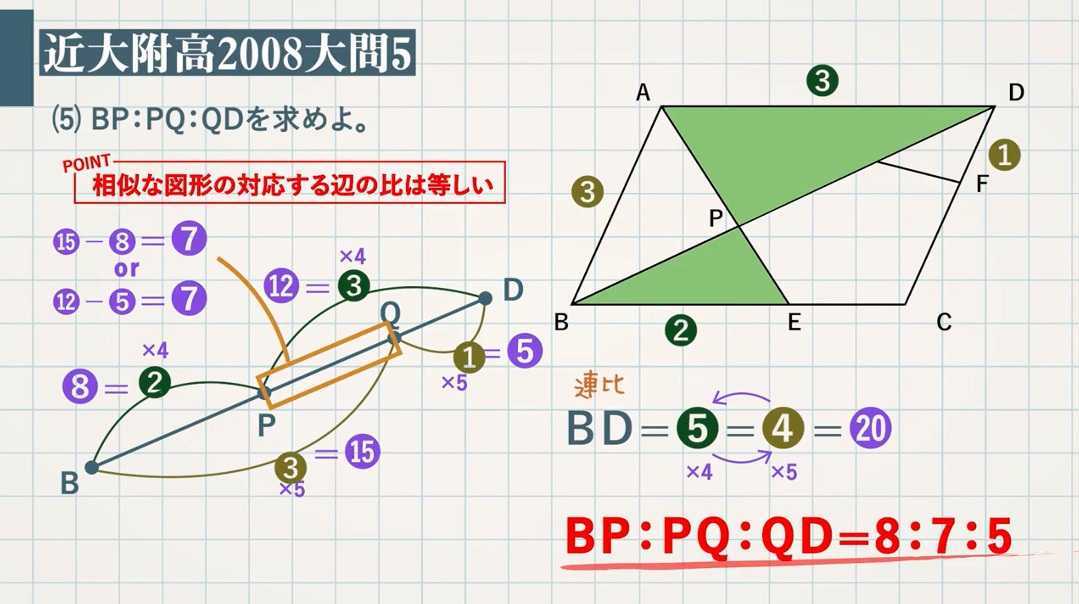 2 | 2 |
 2 | 2 | 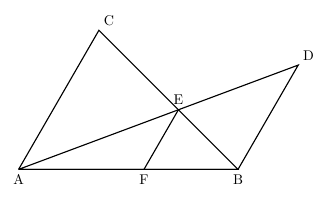 2 |
 2 |  2 | 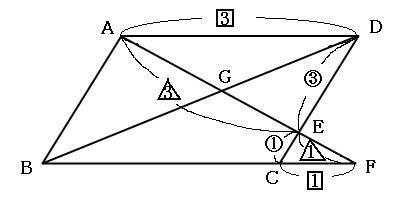 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
 2 |  2 |
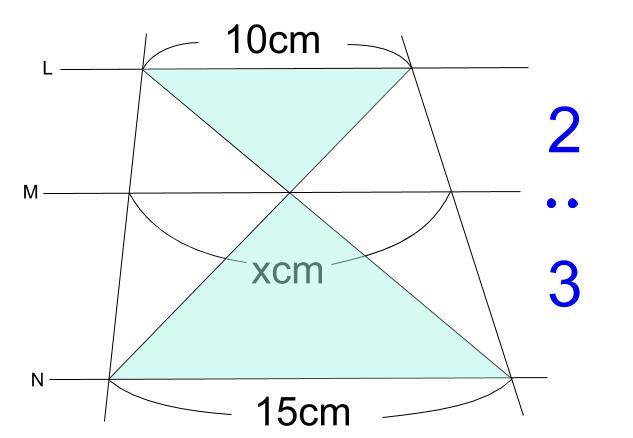
正方形と直角三角形 正方形を作る 正六角形 積 積の法則 接点 千 選挙 線対称 センチメートル 線分 線分図 線分の比 平行四辺形の面積 平行線と線分の比で下の写真の三角形の比が 22+3=25 とあったのですがこの式はいったいどういう理屈で出てきたかわかりません 何故22という 比が出てきて更に3を足すのですか、何
Incoming Term: 平行線と線分の比 平行四辺形,
コメント
コメントを投稿